实现Snapshot

当无同步更新时，scan返回的是当前所有寄存器中的值

当有同步更新时，返回的是last written value或concurrent update value

类似于regular

实现Atomic

思路：通过两个相同的collect，确保这两次操作期间没有更新，从而找到一个linearization point

注意：“相同的collect”不仅指值相同，还需要timestamp相同，否则反例见Snapshot的timestamp

实现Wait-free

上面的算法不是wait-free，因为当有多个进程同步调用scan时，可能发生这样的情况：

p1特别快，不停地更新
p2很慢，想要scan，但每次由于p1的更新，temp1总不等于temp2，无法返回

解决思路通常是，让快的进程多做点事。这里如果让p1每次更新时，还要scan，那么p2即使自己无法完成scan，但可以直接抄p1 scan的结果，就有机会返回，从而达到整体的wait-free。具体算法如下：

这里 if( t3=t2 ) 比较的是自己这次和上次的结果，如果一样，可以返回

而 if( t3[j,2] ≥ t1[j,2]+2 ) 比较的是其它进程，它这次的结果有没有比第一次新？如果是，则说明这两个时间点之间有过一次完整的scan，可以抄过来直接用

为什么≥2（一个反例）

如果将( t3[j,2] ≥ t1[j,2]+2 )变成( t3[j,2] ≥ t1[j,2]+1 )，无法保证一次完整的scan，可能发生这样的情况：

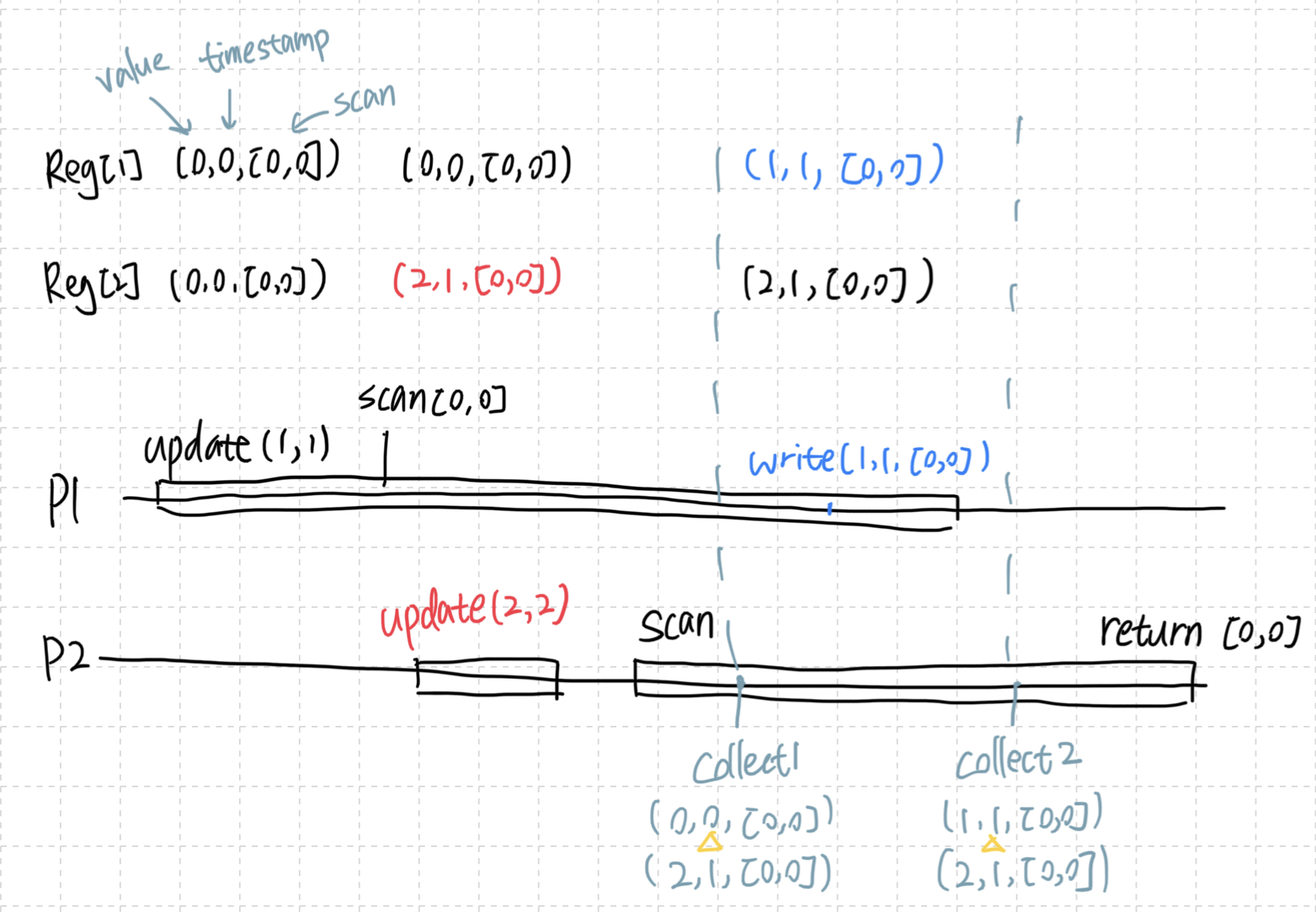
即，虽然有一次更新，但这个更新可能开始于很久很久以前。如果是≥2，则可以避免。

实现Anonymous

几个不同：

上面是一个process对应一个Reg（如process1只会更新Reg1）；这里不必一一对应，从而保证anonymous
上面每个process有自己的local timestamp，每次加1；这里用一个共享的weak counter

（这里写的是n+1，后来TA说其实n就够了）

为什么n（一个反例）

（from last exercise session）

如果2个相同的collect就返回，假设：

N个process同时开始，都拿到了相同的timestamp t1
process N想要scan
process 1 ~ N-1想要update（在write之前，都进行了scan，记为s1。s1=s0）

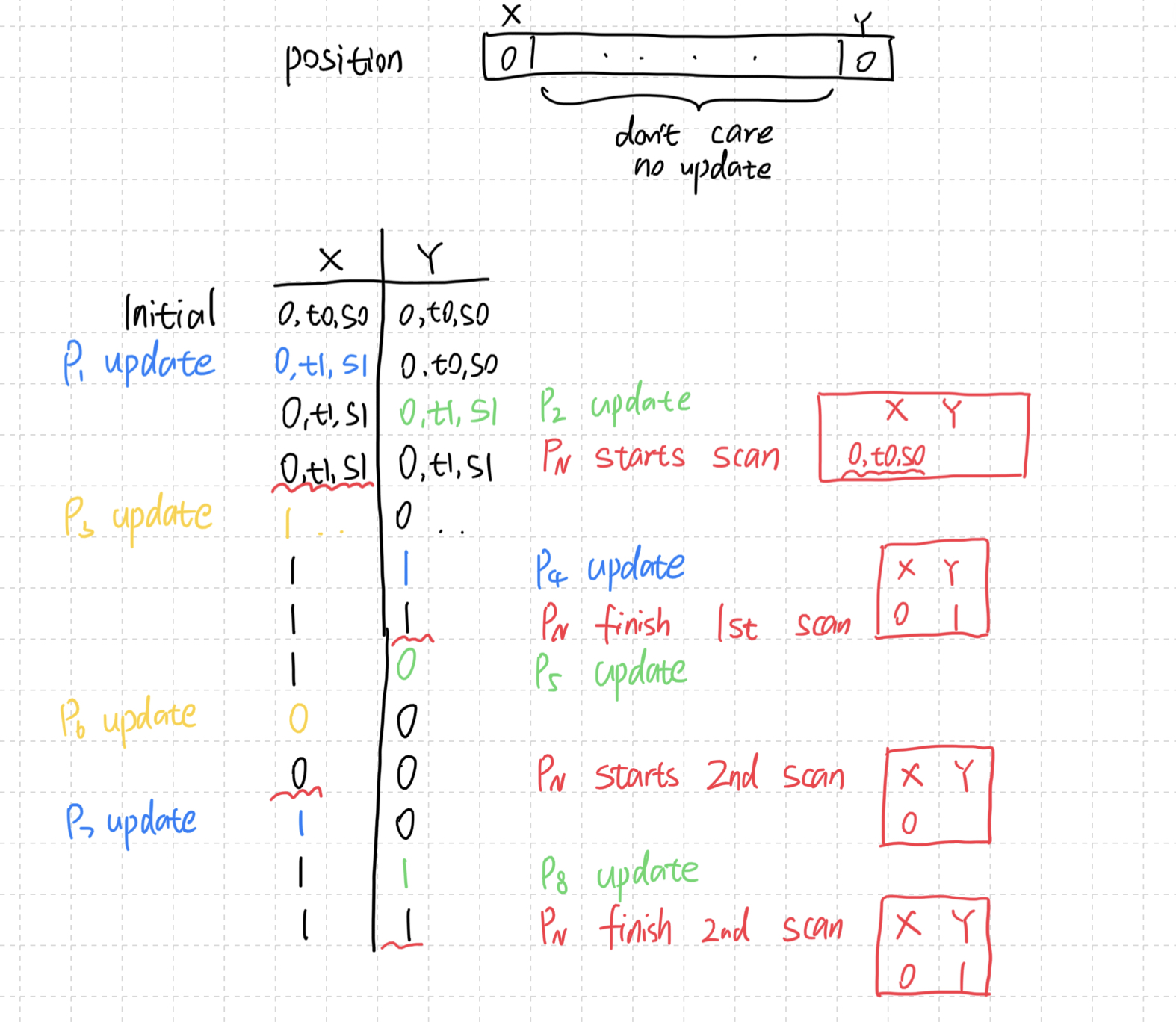
PN两次扫描得到了相同的[0,1]，会返回这个值
但是观察整个过程中X和Y位置的值，从来没有出现过[0,1]。这个scan无法linearize到一个时间点，违背Atomic
如果等N次相同的更新，可以避免该问题（因为其它N-1个process相同的timestamp已经用完了）

比较

非Anonymous情况：

process和Reg一一对应
非weak counter，每次操作都有唯一的timestamp
判断自己的collect是否可以返回 (连续2次collect相同)
- 连续2次collect，所有值相同，所有timestamp相同
- 即可保证这两次collect之间有一次完整的scan
判断能否抄别人的scan (某人的ts ≥ 自己开始时的ts+2)
- ts是每个process本地的，至少2才能保证没有“睡了很久刚醒”的情况

Anonymous情况：

process和Reg并非一一对应，一个Reg可能同时被N个process更新
weak counter，N个process可能同时获得相同的timestamp
判断自己的collect是否可以返回 (连续n次collect相同)
- 连续n次collect，所有值相同，所有timestamp相同
- 为什么是n？极限情况：
  - 所有N个process拿到了相同的timestamp，写相同值，写到同一个Reg中
  - 除自己以外，最多可能有N-1个一模一样的更新
  - 但如果读到了N个相同的结果，说明剩余N-1个process中，至少有一个更新了两次。这两次之间是一个完整的scan
- What If…?
  - 把Weak counter改成Strong counter，不会拿到相同的timestamp -> 2次连续collect相同即可
  - 仍是Weak counter，但最多10个process拿到相同的timestamp -> 10次连续collect相同即可
判断能否抄别人的scan ( 某处的ts ≥ 自己开始时的ts+1 )
1. 细节：这里开始时的ts也是从Weak counter获得的，而不是collect()得到的（即，不是update()写入的）
2. Weak counter的性质保证，如果ts更大，该操作一定更晚发生，不会有“睡了很久刚醒”的情况
  - 甚至可以是 ( 某处的ts ≥ 自己开始时的ts )，只要不小于即可，Weak counter的性质可保证完整的scan（Exercise 8 Problem 2）

总结

判断能否用自己collect的结果，需要比较两个collect是否相同（包括值和timestamp），当timestamp可能重复时，还需要排除重复情况。

判断能否抄别人的结果，需要确保产生这个结果的scan发生在自己开始之后，根据timestamp获取方式的不同（local和shared weak counter），比较时大多少也有所区别。

附

TA的解释

关于Atomic，和实现linearizable的思路

Weak counter facts (perspective of an individual process):

- After I get a value (return) from the weak counter by calling wInc(), at most N-1 other processes can still obtain a value less or equal to that.

This is true because at most N-1 other processes can be concurrently executing with me (there are at most N processes after all, me being one of them), and specifically, executing wInc() on that same counter (e.g. they could have been about to return from wInc()). A weak counter guarantees that if some process calls wInc after I return from wInc (Correctness) that process will get a higher timestamp so adding to the previous fact, at most N-1 processes might still get a lower or equal value to the one I have just obtained.

Now, the goal of the atomic snapshot (anonymous or not) is to return a read of the entire array that is linearizable. We break correctness if we somehow return an array that is not linearizable. For example, take the following history (sequence of states) for an array of size 2:

S1: [0, 0] -> S2: [1, 0] -> S3: [1, 1] -> S4: [1, 0] -> S5: [0, 0]

At no point in time did the array ever have the state [0, 1]. If we ever were to return that state in the scan() operation, it would break correctness. However, this could happen if we were doing a naive approach where we simply collected once (read e.g. left to right): We read the first register at S1, sleep during S2, read the second register at S3, and finally return [0, 1].

The key point is that this problem arises only if some other process writes while we are reading: if we could guarantee that, when we collect, no process wrote on any register of the array, we would be free to return the result of that collect.

The non-anonymous snapshot solves this problem in two manners:

- We add timestamps to each register

- We collect twice and only return the result if and only if the timestamps of all registers have not changed.

This implies that no register wrote on the array between the first and second collect (and that is the scan’s linearization point). Why? Because each process has its own register, therefore each register’s timestamp is monotonically increasing. If there is a write to the register, the timestamp necessarily increases (by one). By negation, if the timestamp did not increase, there was no write.

Can we make the same argument for the anonymous snapshot’s algorithm? The answer is no. The difficulty comes because the model is different: the anonymous snapshot allows any process to update any register. If we constrained or assigned processes to a few or their own register, we would break anonymity. The consequence is that, for each register, its timestamp is no longer monotonically increasing (because of counter is weak), so even if two reads return the same value for that register there might have been a write in between.

However, even if it is not monotonically increasing, it necessarily increases after every N writes (see Weak Counter facts at the beginning of this explanation). So by collecting N+1 times and getting the same timestamps on all registers, there must necessarily be a point between two of the N+1 collects in which no write to any register could have happened, and we can linearize our scan then.

反例2

Consider an anonymous snapshot object with M = 2, i.e. only 2 slots. Suppose process p is performing a scan operation. Suppose also that the scan operation consists of only 2 collects, as you mention, and not N as the original algorithm implies, and that process p obtains timestamp t. Suppose all other N-1 processes are performing update operations, have all obtained the same timestamp t’ < t and scan S, and are about to write to their corresponding register (paused just before writing).

Since N can be made arbitrarily large (and thus so can N-1), I can use any constant number of processes from this group in my counter example. More specifically, in these conditions I can choose to apply any number of writes of any value to any position of the snapshot at any point during process p’s scan, with the restriction that the timestamp value written is t’ and the scan is S. Taking this into account, consider the following sequence of operations and state of the snapshot:

[empty, empty] - initial value

[(0, t’, S), empty] - process q1 writes (v = 0, i = 0)

[(0, t’, S), (0, t’, S)] - process q2 writes (v = 0, i = 1)

[(0, t’, S), (0, t’, S)] - process p reads the first register. first collect -> (0, t’, S)

[(1, t’, S), (0, t’, S)] - process q3 writes (v = 1, i = 0)

[(1, t’, S), (1, t’, S)] - process q4 writes (v = 1, i = 1)

[(1, t’, S), (1, t’, S)] - process p reads the second register. first collect -> (1, t’, S)

[(1, t’, S), (0, t’, S)] - process q5 writes (v = 0, i = 1)

[(0, t’, S), (0, t’, S)] - process q6 writes (v = 0, i = 0)

[(0, t’, S), (0, t’, S)] - process p reads the first register. second collect -> (0, t’, S)

[(1, t’, S), (0, t’, S)] - process q7 writes (v = 1, i = 0)

[(1, t’, S), (1, t’, S)] - process q8 writes (v = 1, i = 1)

[(1, t’, S), (1, t’, S)] - process p reads the second register. second collect -> (1, t’, S)

In the previous execution, process p returns [0, 1] as the result of the scan operation (2 identical collects). However, at no point in time was the state of the snapshot ever [0, 1] indicating that the read of the snapshot is not linearizable.

Finally, note that the authors of the paper are not claiming a lower bound on the number of reads that have to be realized to have an atomic snapshot. They are claiming an upper bound (N collects -> N x M reads). Maybe with some other algorithm, a strong counter or the like, you would be able to do it with less reads, but the present algorithm fails for just 2 collects as I’ve show above.